Kurrent Numbers
Below are examples of how a scribe would have formed Kurrent numbers. This is useful when trying to decipher hard to read numbers or numbers that are similar to each other.
Use the buttons to jump to a specific letter to study.
1
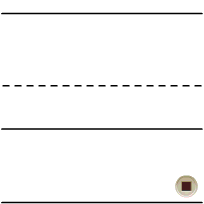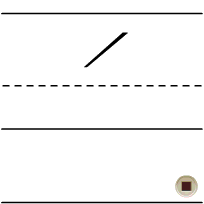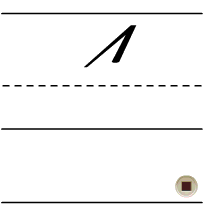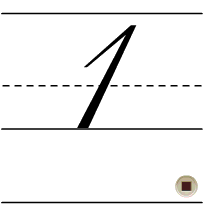
The Kurrent 1 almost always has a diagonal stroke coming out of the top left of the main stem. This diagonal stroke may extend as far as the midline or even the baseline.
Examples:
2

The Kurrent 2 starts with a downward loop that extends diagonally to the left until the baseline, and then culminates in an upward then downward curve in the shape of a horizontal s.
Examples:
3

The Kurrent 3, like the Kurrent z, is formed by two loops, one on top of the other. There might be a small loop in the middle where the two big loops connect. To differentiate this number from a Kurrent 5, look for the top loop which always curves to the left.
Examples:
4

The Kurrent 4 is formed by an L-shaped stroke over the midline intersecting a main vertical stem. Sometimes the L-shaped stroke goes under the midline and may even almost touch the baseline.
Examples:
5

Starting at the top, the Kurrent 5 extends down to the midline in a straight line and then loops backward until it at least touches the baseline, finally a curve is included on the top. The big loop on the bottom is usually proportional to the upper part of the number. More often than not, the Kurrent 5 is very slanted. To avoid confusion with the Kurrent 3, always look for a loop that extends to the right.
Examples:
6

The Kurrent 6 is written as a single line that starts at the top and then curves downward and to the right, generally forming a closed loop at the midline. Sometimes this loop does not close completely.
Examples:

|
7

One of the main characteristics of the Kurrent 7 is the "roof" extending to the upper left of the main stem. This roof looks something like a horizontal s, or perhaps a backward loop with a descending diagonal line to the left. The cross-stroke at the midline is optional, and for this reason the Kurrent 7 might be confused sometimes with the Kurrent 9.
Examples:

|
8

The Kurrent 8 is usually a continuous set of two closed loops, one on top of the other. The top loop might not always be completely closed.
Examples:
9

Occasionally the Kurrent 9 might be confused with the Kurrent 7. The only difference is that the upper loop in this number is always closed.
Examples:

| 
|
0

The Kurrent 0 is simply a large closed loop. It may connect to the numbers before or after it from the top, where it will always start and end.
Examples:

|
These numbers may be easily practiced with our handwriting practice sheets.














